The following program calculates the minimum point of a multi-variable function using the grid search method. This method performs a multi-dimensional grid search. The grid is defined by a multiple dimensions. Each dimension has a range of values. Each range is divided into a set of equal-value intervals. The multi-dimensional grid has a centroid which locates the optimum point. The search involves multiple passes. In each pass, the method local a node (point of intersection) with the least function value. This node becomes the new centroid and builds a smaller grid around it. Successive passes end up shrinking the multidimensional grid around the optimum.
The program prompts you to enter for each variable (i.e. dimension):
1. The values that define the lower and upper limits of a search range for a variable,
2. The number of divisions for a range.
3. The minimum range value, used to determine when to stop searching..
The program also asks you to enter the function tolerance. The program uses this value to possible stop iterating when successive best function values are close enough.
The program displays intermediate values for the function and the variables. The program displays the following final results:
1. The coordinates of the minimum point.
2. The minimum function value.
3. The number of iterations
The current code finds the minimum for the following function:
f(x1,x2) = 10 + (x1 ^ 2 - 1) ^ 2 + (x2^2 - 2) ^ 2
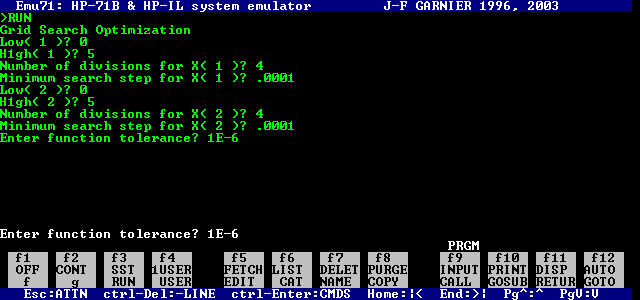
Here is a sample session to solve for the optimum of the above function. The first image shows the input:

The second image shows the output:
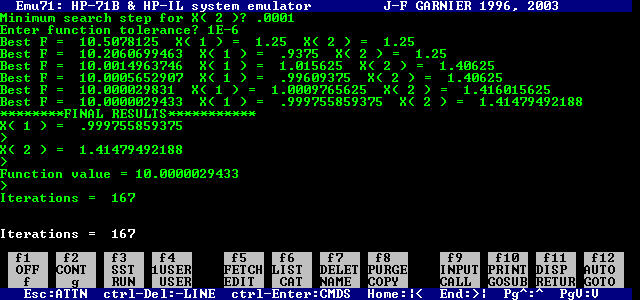
Here is the BASIC listing:
10 ! Grid Search Optimization
20 !
30 ! Routine performs grid search. The iterations relocate the centroid to be the current optimum.
40 ! The routine srhinks the grid size in each iteration.
50 !
60 !
70 N = 2
80 I9 = 5000000
90 DIM N0(N)
100 DIM X(N), X9(N), X5(N)
110 DIM D(N), D0(N)
120 DIM L0(N), H1(N)
130 DISP "Grid Search Optimization" @ WAIT 3
140 For I = 1 To N
150 ! Get lower range
160 DISP "Low(";I;")";
170 INPUT L0(I)
180 ! Get upper range
190 DISP "H1gh(";I;")";
200 INPUT H1(I)
210 ! Calculate center
220 X5(I) = (L0(I) + H1(I)) / 2
230 ! Get number of divisions
240 DISP "Number of divisions for X(";I;")";
250 INPUT N0(I)
260 ! Calculate initial search step
270 D(I) = (H1(I) - L0(I)) / N0(I)
280 ! Get minimum search step
290 DISP "Minimum search step for X(";I;")";
300 INPUT D0(I)
310 X(I) = L0(I) ! set initial X
320 Next I
330 INPUT "Enter function tolerance? "; E
340 ! calculate and display function value at initial point
350 CALL MyFx(X5, N, B)
360 IF B > 0 THEN L = 100 + B ELSE L = B - 100
370 I0 = 0
380 REM DO1
390 REM DO2
400 I0 = I0 + 1
410 CALL MyFx(X, N, F)
420 If F >= B Then 480
430 L = B
440 B = F
450 For I = 1 To N
460 X9(I) = X(I)
470 Next I
480 REM ENDIF1
490 !*****************************************************
500 ! The next For loop implements a programming tricks
510 ! that simulated nested loops using just one For loop
520 !*****************************************************
530 ! search next grid node
540 For I = 1 To N
550 If X(I) < H1(I) Then 580
560 If I < N Then X(I) = L0(I) Else 650
570 GOTO 610
580 REM ELSE2
590 X(I) = X(I) + D(I)
600 GOTO 630
610 REM ENDIF2
620 Next I
630 REM FOR1
640 GOTO 390
650 REM EXITDO2
660 I0 = I0 + 1
670 DISP "Best F = "; B;" ";
680 For I = 1 To N
690 DISP "X(";I;") = ";X9(I);" ";
700 X5(I) = X9(I)
710 D(I) = D(I) / N0(I)
720 L0(I) = X5(I) - D(I) * N0(I) / 2
730 H1(I) = X5(I) + D(I) * N0(I) / 2
740 X(I) = L0(I) ! reset array X
750 Next I
760 DISP ""
770 G0 = 0
780 For I = 1 To N
790 If D(I) > D0(I) Then G0 = 1
800 Next I
810 If (Abs(B - L) <= E) OR (I0 > I9) Then G0 = 0
820 IF G0 = 1 THEN 380
830 REM EXITDO2
840 DISP "********FINAL RESULTS***********"
850 For I = 1 To N
860 DISP "X(";I;") = ";X9(I) @ PAUSE
870 Next I
880 DISP "Function value =";B @ PAUSE
890 DISP "Iterations = ";I0
900 END
910 SUB MyFx(X(), N, R0)
920 R0 = 10
930 For K = 1 To N
940 R0 = R0 + (X(K) ^ 2 - K) ^ 2
950 Next K
960 End Sub
Copyright (c) Namir Shammas. All rights reserved.