The following program calculates the minimum point of a multi-variable function using random search method. This method starts with an initial point and a search radius for each variable. The algorithm searches for a better optimum point within the search radius. This approach allows the search to drift towards the optimum point without being confined to absolute search ranges.
The program prompts you to enter:
1. The initial value for each variable
2. The search radius for each variable
3. The tolerance for the function value
The program displays the following results:
1. The coordinates of the minimum value.
2. The minimum function value.
3. The number of iterations
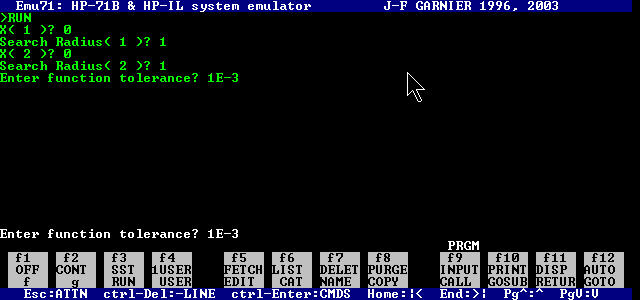
Here is a sample session to find the minimum of f(x) = 10 + (x1^2-1)^2 + (x2^2-2)^2 using the initial point of [0, 0], search radius of [1,1], and function tolerance of 1e-3. Remember your results are most likely to be different. The output show next is that of the EMU71 emulator for the HP-71B.
The first image shows the input:

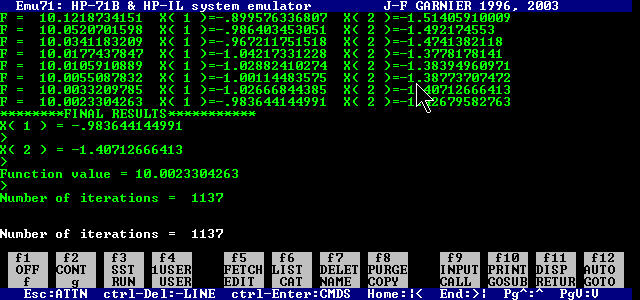
The next image shows the output:
Here is the BASIC listing:
10 ! Random Drift Optimization
20 N = 2
30 I9 = 10000
40 RANDOMIZE
50 !
60 ! This method implements a random walk algorithm.
70 ! The method starts with an initial point and a radius of search
80 ! Random numbers are generated within the radius of search allowing
90 ! for the current optimum to "drift" towards a minimum.
100 ! THIS METHOD HAS NO PREDEFINED RANGES, making it more flexible
110 ! to find an optimum, given enough iterations
120 !
130 DIM X(N), X9(N), R(N), X0(N)
140 RANDOMIZE
150 For I = 1 To N
160 DISP "X(";I;")";
170 INPUT X0(I)
180 DISP "Search Radius(";I;")";
190 INPUT R(I)
200 X9(I) = X0(I)
210 Next I
220 INPUT "Enter function tolerance? "; E
230 ! calculate and display function value at initial point
240 CALL MyFx(X9, N, B)
250 L = SGN(B) * (100 + 100 * B)
260 I0 = 0
270 REM DO
280 I0 = I0 + 1
290 If I0 > I9 Then 470
300 For I = 1 To N
310 X(I) = X9(I) + (Rnd - 0.5) * R(I)
320 CALL MyFx(X, N, F)
330 If F >= B Then 440
340 X9(I) = X(I)
350 L = B
360 B = F
370 DISP "F = "; B;" ";
380 For J = 1 To N
390 DISP "X(";J;")=";X(J);" ";
400 Next J
410 DISP
420 ! test function value convergence
430 If Abs(B - L) < E Then 470
440 REM END_IF
450 Next I
460 GOTO 270
470 REM EXIT_DO
480 DISP "********FINAL RESULTS***********"
490 For I = 1 To N
500 DISP "X(";I;") = ";X9(I) @ PAUSE
510 Next I
520 DISP "Function value =";B @ PAUSE
530 DISP "Number of iterations = "; I0
540 END
550 SUB MyFx(X(), N, F0)
560 F0 = 10
570 For K = 1 To N
580 F0 = F0 + (X(I) ^ 2 - K) ^ 2
590 Next K
600 END SUB
You can customize the above listing by
changing the definition of function in the subroutine MyFX. The current listing
is set to solve the following equation:f(x1, x2) = 10 + (x1^2-1)^2 + (x2^2+4)^2
The above function has a minimum at x1=+/-1 and x2=+/-1.4142.
Copyright (c) Namir Shammas. All rights reserved.