The following program calculates the minimum point of a multi-variable function using the grid search method. This method performs a multi-dimensional grid search. The grid is defined by a multiple dimensions. Each dimension has a range of values. Each range is divided into a set of equal-value intervals. The multi-dimensional grid has a centroid which locates the optimum point. The search involves multiple passes. In each pass, the method local a node (point of intersection) with the least function value. This node becomes the new centroid and builds a smaller grid around it. Successive passes end up shrinking the multidimensional grid around the optimum.
The program prompts you to enter for each variable (i.e. dimension):
1. The values that define the lower and upper limits of a search range for a variable,
2. The number of divisions for a range.
3. The minimum range value, used to determine when to stop searching..
The program also asks you to enter the function tolerance. The program uses this value to possible stop iterating when successive best function values are close enough.
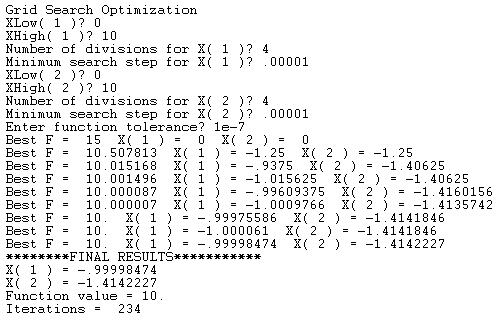
The program displays intermediate values for the function and the variables. The program displays the following final results:
1. The coordinates of the minimum point.
2. The minimum function value.
3. The number of iterations
The current code finds the minimum for the following function:
f(x1,x2) = 10 + (x1 ^ 2 - 1) ^ 2 + (x2^2 - 2) ^ 2
Here is a sample session to solve for the optimum of the above function:

Here is the BASIC listing:
! Grid Search Optimization
OPTION TYPO
OPTION NOLET
DECLARE NUMERIC MAX_VARS, MAX_ITER
DECLARE NUMERIC N, I, J, Iter
DECLARE NUMERIC F, XX
DECLARE NUMERIC BestF, LastBestF, EPSF
DECLARE NUMERIC bGoOn, bTrue, bFalse
DIM NumDiv(1)
DIM X(1), XBest(1), XCenter(1)
DIM Delta(1), MinDelta(1)
DIM XLo(1), XHi(1)
bTrue = 1
bFalse = 0
SUB MyFx(X(), N, funRes)
LOCAL I
funRes = 10
For I = 1 To N
funRes = funRes + (X(I) ^ 2 - I) ^ 2
Next I
End Sub
! Grid Search Optimization
!
! Routine performs grid search. The iterations relocate the centroid to be the current optimum.
! The routine srhinks the grid size in each iteration.
!
!
MAX_VARS = 2
MAX_ITER = 5000000
MAT REDIM NumDiv(MAX_VARS)
MAT REDIM X(MAX_VARS), XBest(MAX_VARS), XCenter(MAX_VARS)
MAT REDIM Delta(MAX_VARS), MinDelta(MAX_VARS)
MAT REDIM XLo(MAX_VARS), XHi(MAX_VARS)
N = MAX_VARS
PRINT "Grid Search Optimization"
For I = 1 To N
! Get lower range
PRINT "XLow(";I;")";
INPUT Xlo(I)
! Get upper range
PRINT "XHigh(";I;")";
INPUT XHi(I)
! Calculate center
XCenter(I) = (XLo(I) + XHi(I)) / 2
! Get number of divisions
PRINT "Number of divisions for X(";I;")";
INPUT NumDiv(I)
! Calculate initial search step
Delta(I) = (XHi(I) - XLo(I)) / NumDiv(I)
! Get minimum search step
PRINT "Minimum search step for X(";I;")";
INPUT MinDelta(I)
X(I) = XLo(I) ! set initial X
Next I
INPUT PROMPT "Enter function tolerance? ": EPSF
! calculate and display function value at initial point
CALL MyFx(XCenter, N, BestF)
LastBestF = 100 + BestF
Iter = 0
Do
Do
Iter = Iter + 1
CALL MyFx(X, N, F)
If F < BestF Then
LastBestF = BestF
BestF = F
For I = 1 To N
XBest(I) = X(I)
Next I
End If
!*****************************************************
! The next For loop implements a programming trick
! that simulated nested loops using just one For loop
!*****************************************************
! search next grid node
For I = 1 To MAX_VARS
If X(I) >= XHi(I) Then
If I < MAX_VARS Then
X(I) = XLo(I)
Else
Exit Do
End If
Else
X(I) = X(I) + Delta(I)
Exit For
End If
Next I
Loop
Iter = Iter + 1
PRINT "Best F = "; BestF;" ";
For I = 1 To N
PRINT "X(";I;") = ";XBest(I);" ";
XCenter(I) = XBest(I)
Delta(I) = Delta(I) / NumDiv(I)
XLo(I) = XCenter(I) - Delta(I) * NumDiv(I) / 2
XHi(I) = XCenter(I) + Delta(I) * NumDiv(I) / 2
X(I) = XLo(I) ! reset array X
Next I
PRINT
bGoOn = bFalse
For I = 1 To N
If Delta(I) > MinDelta(I) Then bGoOn = bTrue
Next I
If (Abs(BestF - LastBestF) <= EPSF) OR (Iter > MAX_ITER) Then
bGoOn = bFalse
End If
Loop While bGoOn = bTrue
PRINT "********FINAL RESULTS***********"
For I = 1 To N
PRINT "X(";I;") = ";XBest(I)
Next I
PRINT "Function value =";BestF
PRINT "Iterations = ";Iter
END
Copyright (c) Namir Shammas. All rights reserved.